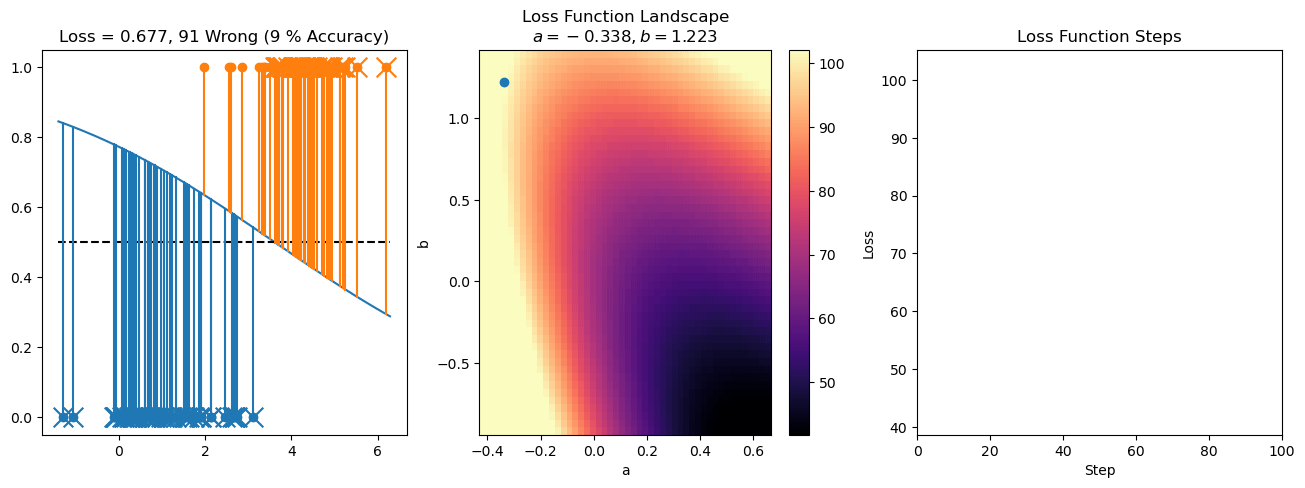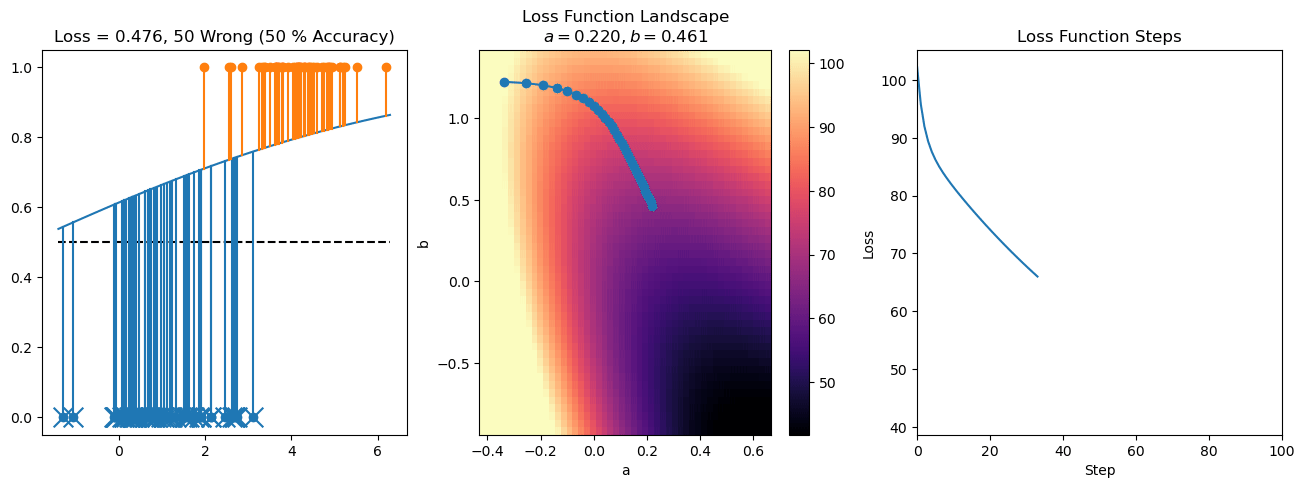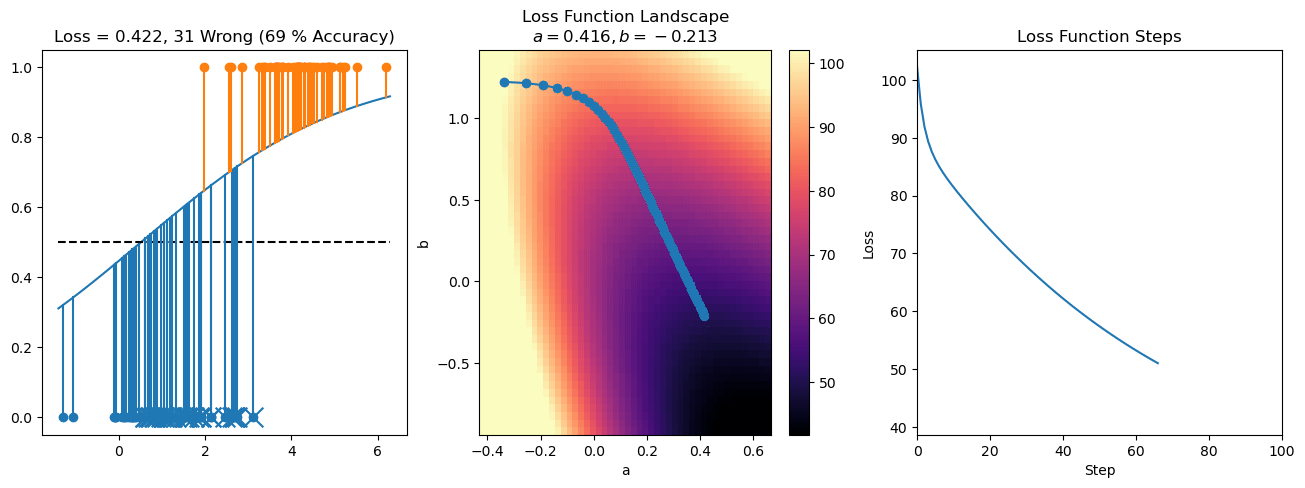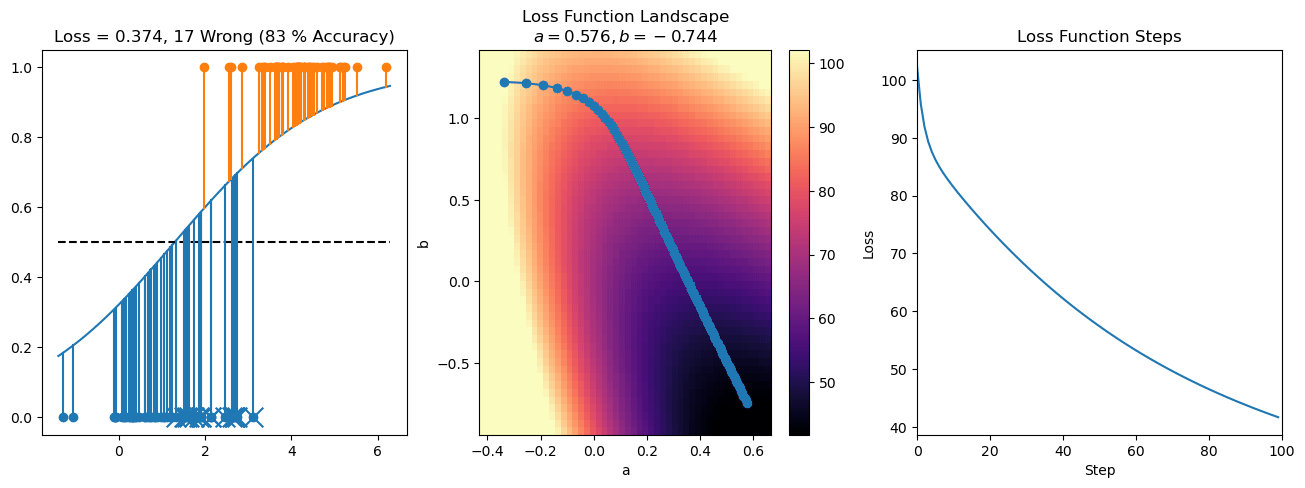
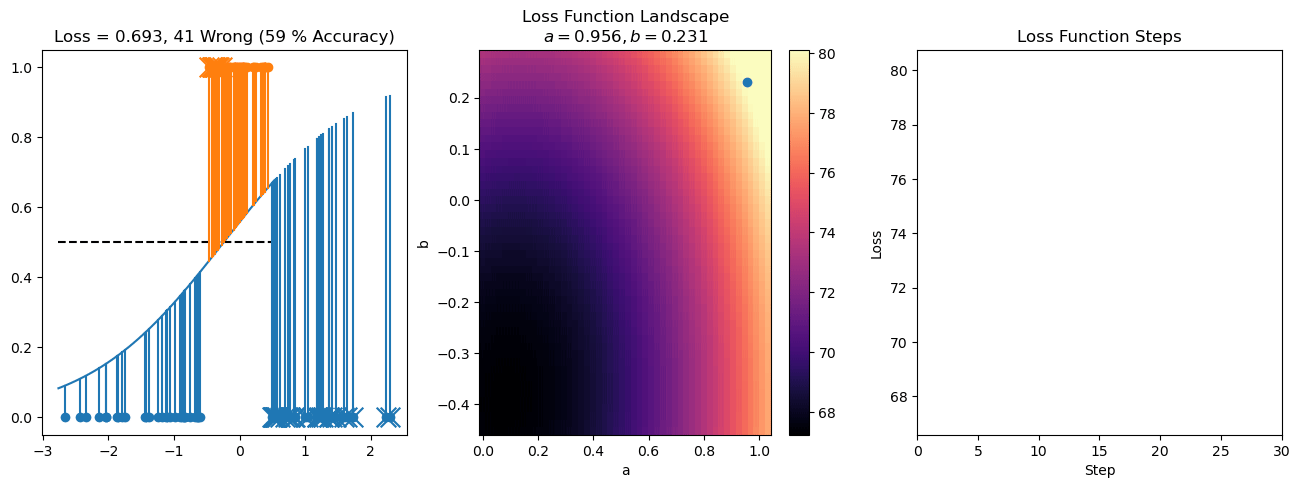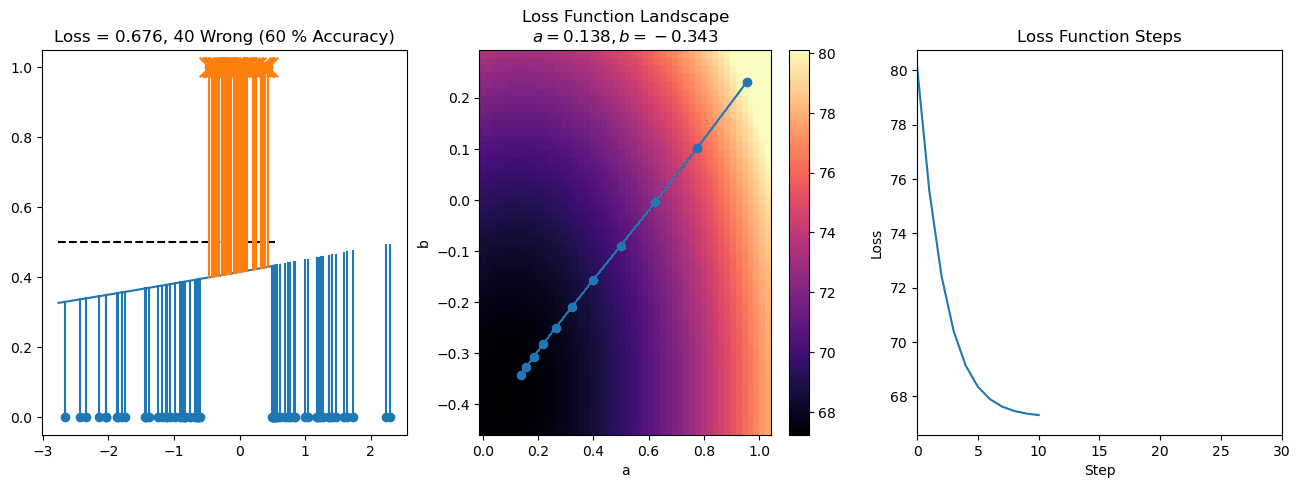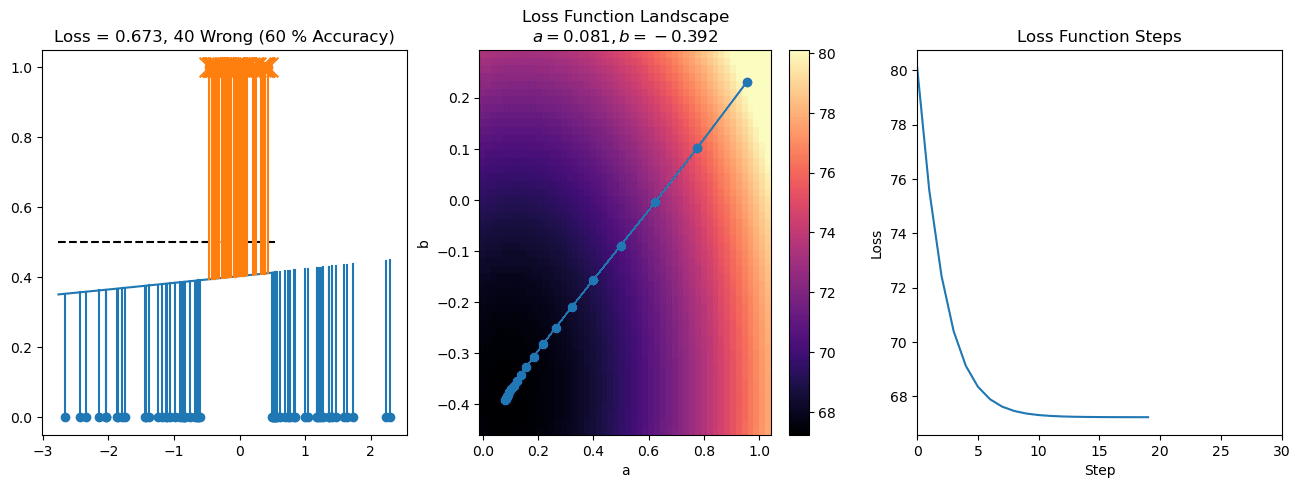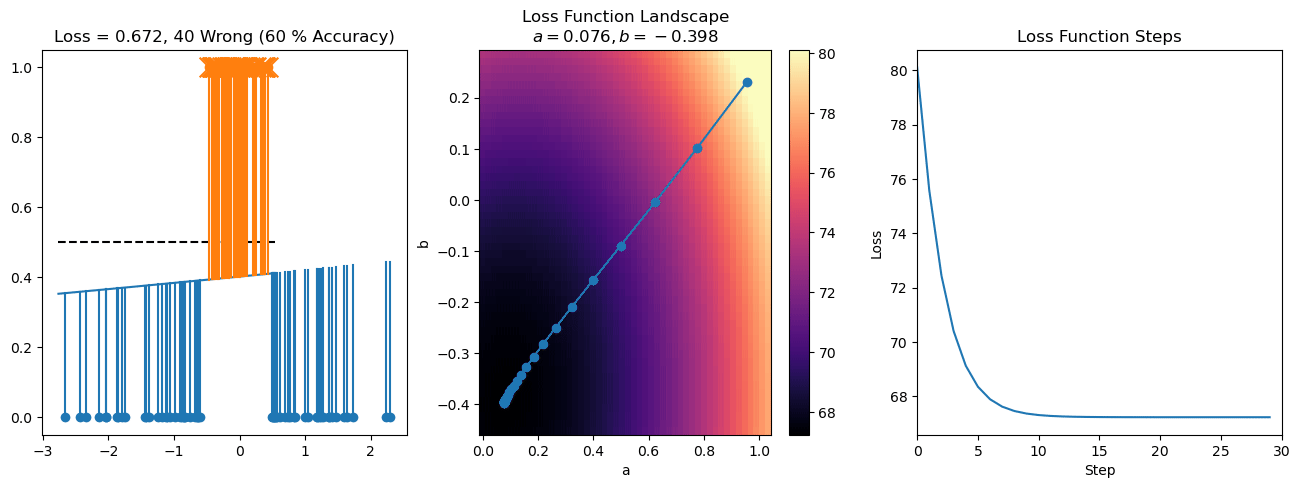
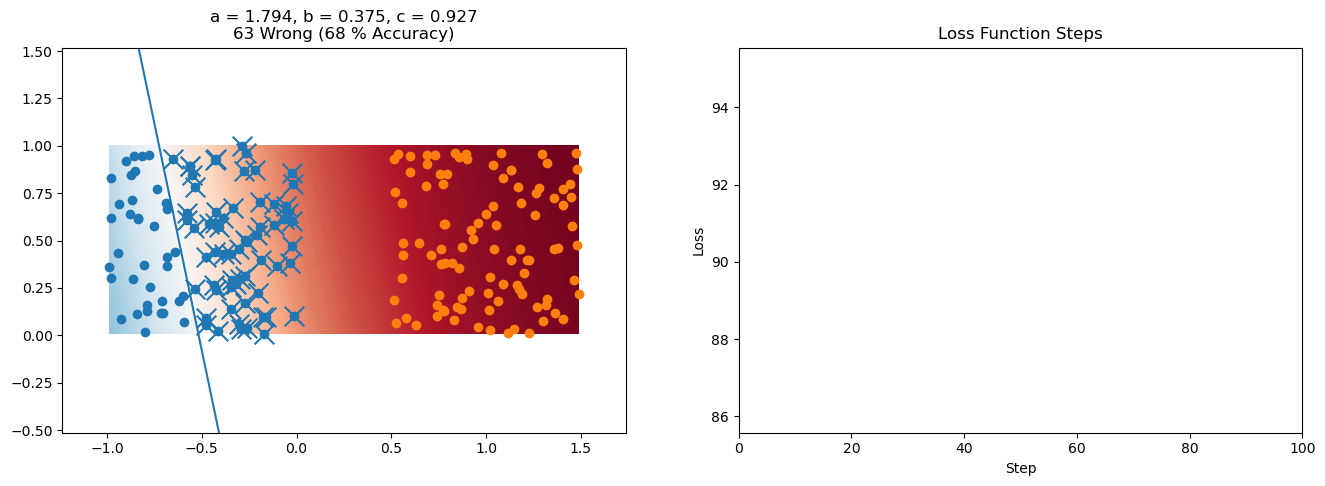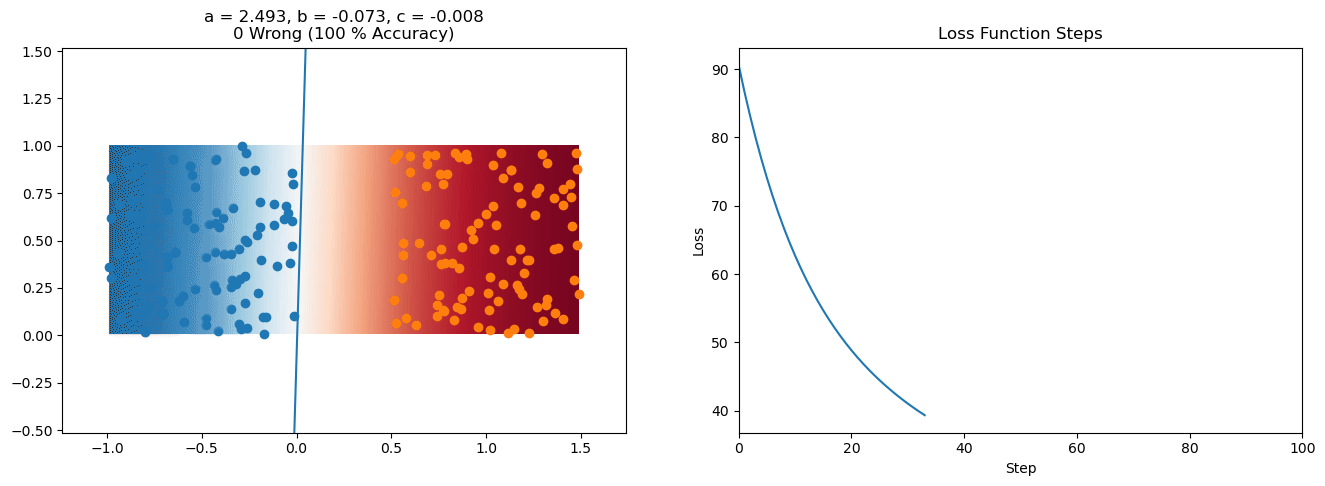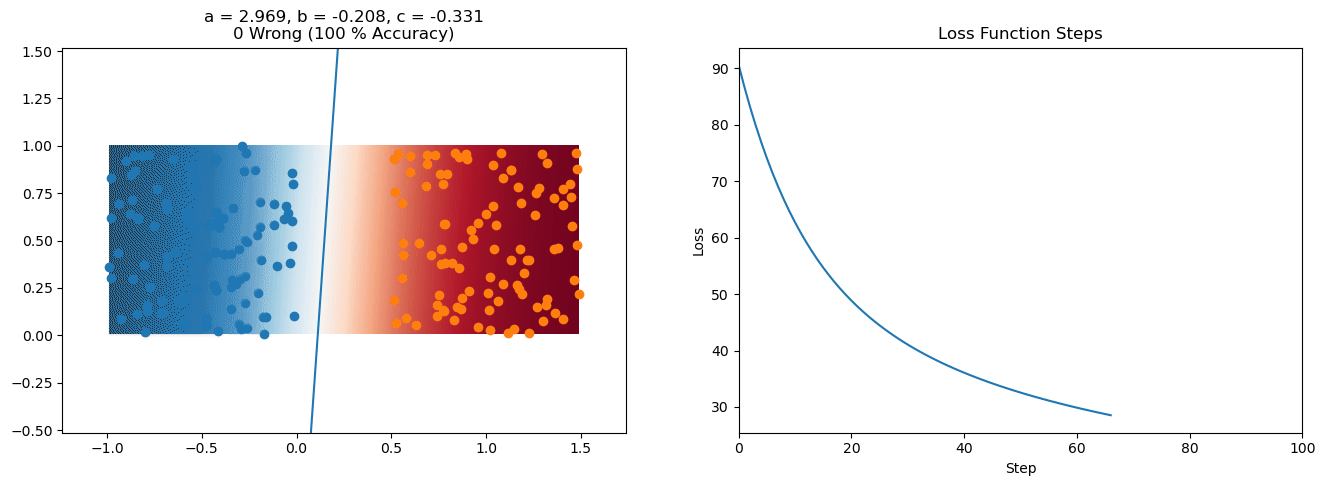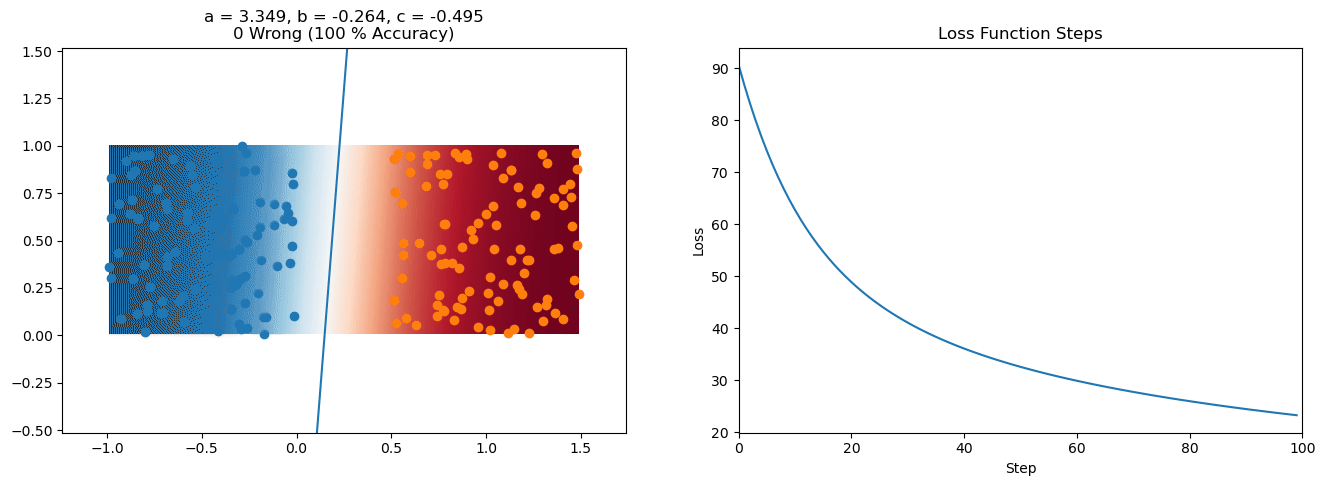
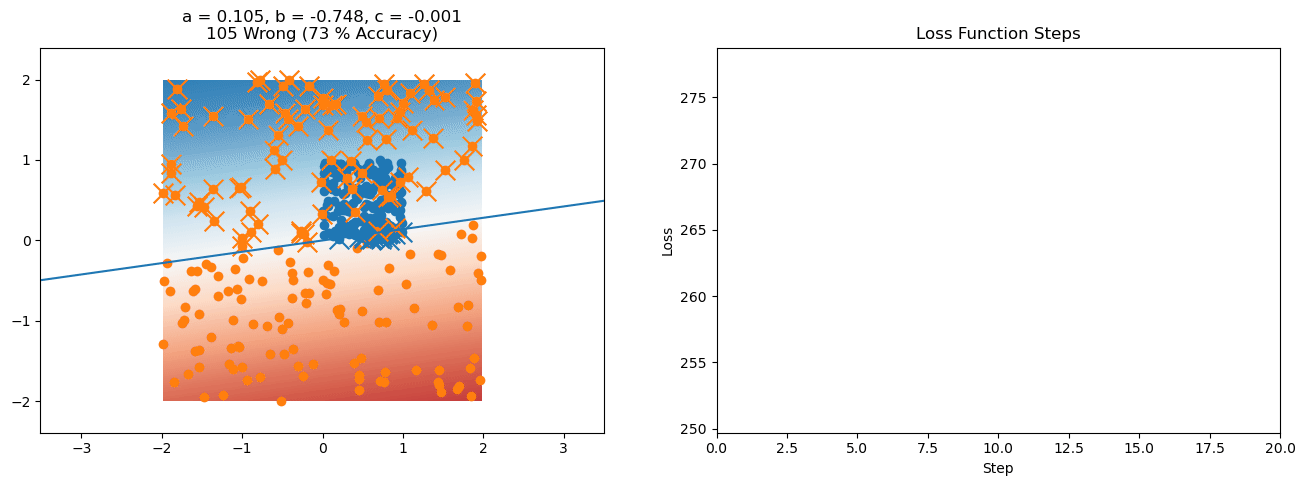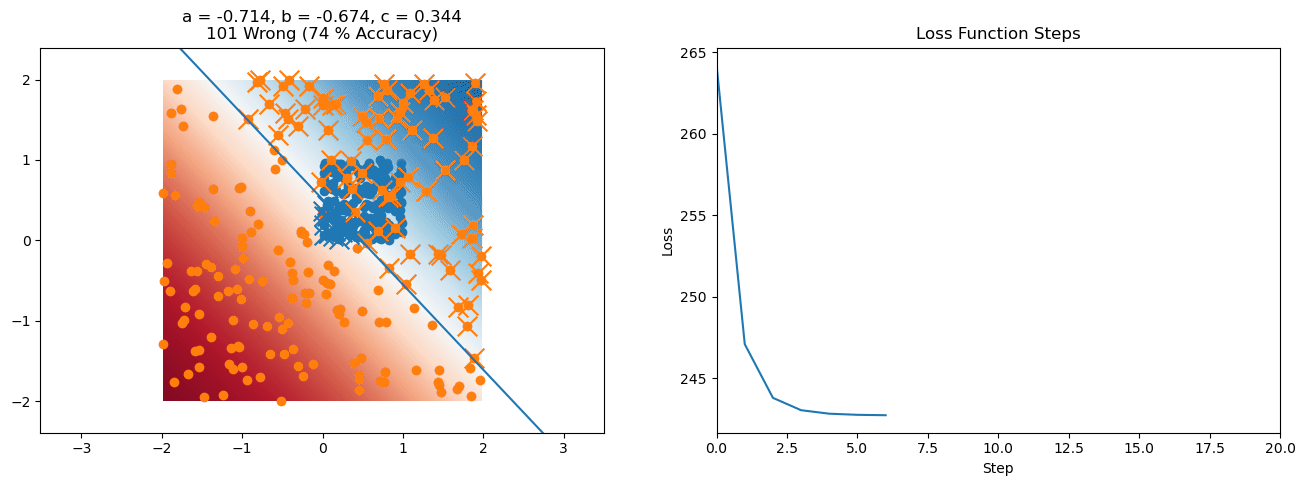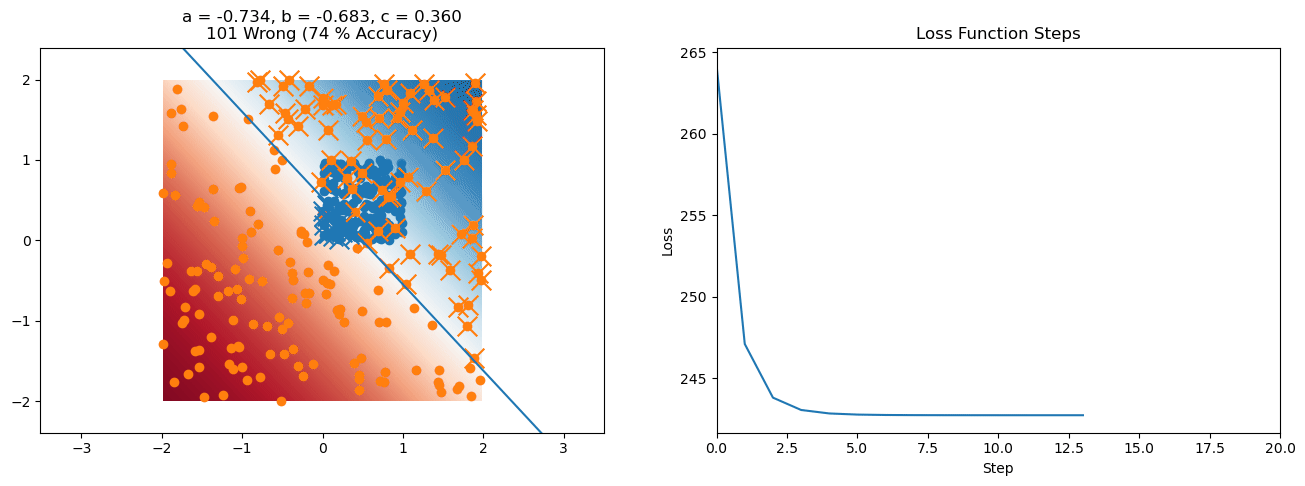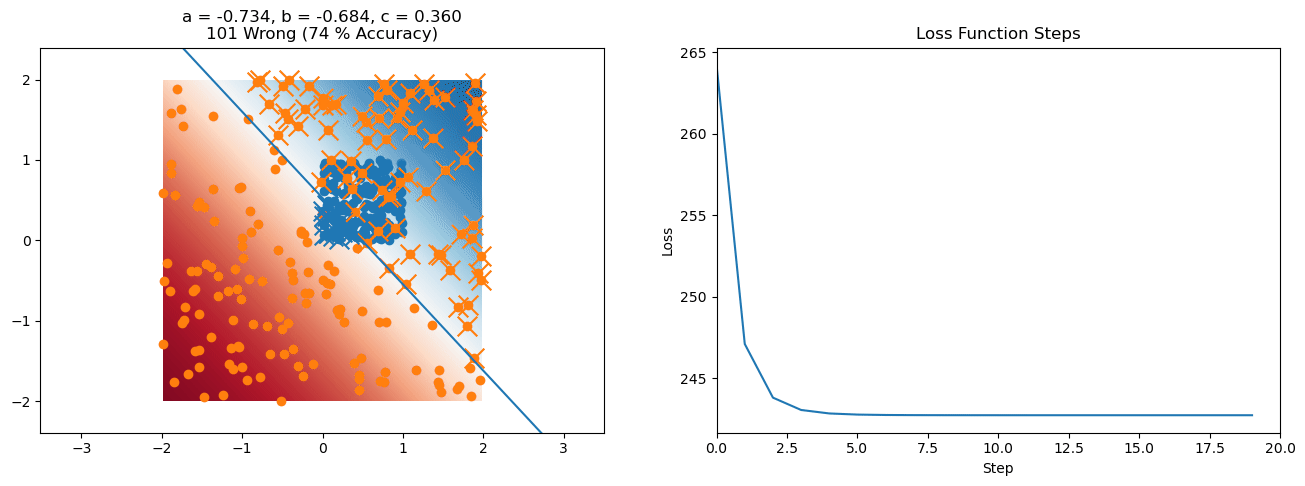
def plot_logistic_regression_predictions(X1, X2, a, b, c):
plt.scatter(X1[:, 0], X1[:, 1])
plt.scatter(X2[:, 0], X2[:, 1])
X = np.concatenate((X1, X2), axis=0)
xmin = np.min(X, axis=0)
xmax = np.max(X, axis=0)
iv = max(xmax[1]-xmin[1], xmax[0]-xmin[0])
resol = 200
mx = 2
xx = np.linspace(xmin[0], xmax[0], resol)
yy = np.linspace(xmin[1], xmax[1], resol)
xx, yy = np.meshgrid(xx, yy)
plt.imshow(logistic(a*xx+b*yy+c), extent=(xmin[0], xmax[0], xmax[1], xmin[1]), cmap='RdBu_r', vmin=0, vmax=1)
p0 = -c*np.array([a, b])/(a**2 + b**2)
v = np.array([-b, a])
mag = np.sqrt(np.sum(v**2))
if mag > 0:
v = v/mag
p = p0 - 2*iv*v
q = p0 + 2*iv*v
plt.plot([p[0], q[0]], [p[1], q[1]])
rg = xmax[0] - xmin[0]
plt.xlim([xmin[0]-0.2*rg, xmax[0]+0.2*rg])
rg = xmax[1] - xmin[1]
plt.ylim([xmin[1]-0.2*rg, xmax[1]+0.2*rg])
wrong = 0
for x in X1:
y = logistic(a*x[0] + b*x[1] + c)
proj = p0 + np.sum(v*(x-p0))*v
#plt.plot([x[0], proj[0]], [x[1], proj[1]], c='C0')
if y > 0.5:
plt.scatter([x[0]], [x[1]], 200, c='C0', marker='x')
wrong += 1
for x in X2:
y = logistic(a*x[0] + b*x[1] + c)
proj = p0 + np.sum(v*(x-p0))*v
#plt.plot([x[0], proj[0]], [x[1], proj[1]], c='C1')
if y < 0.5:
plt.scatter([x[0]], [x[1]], 200, c='C1', marker='x')
wrong += 1
N = X.shape[0]
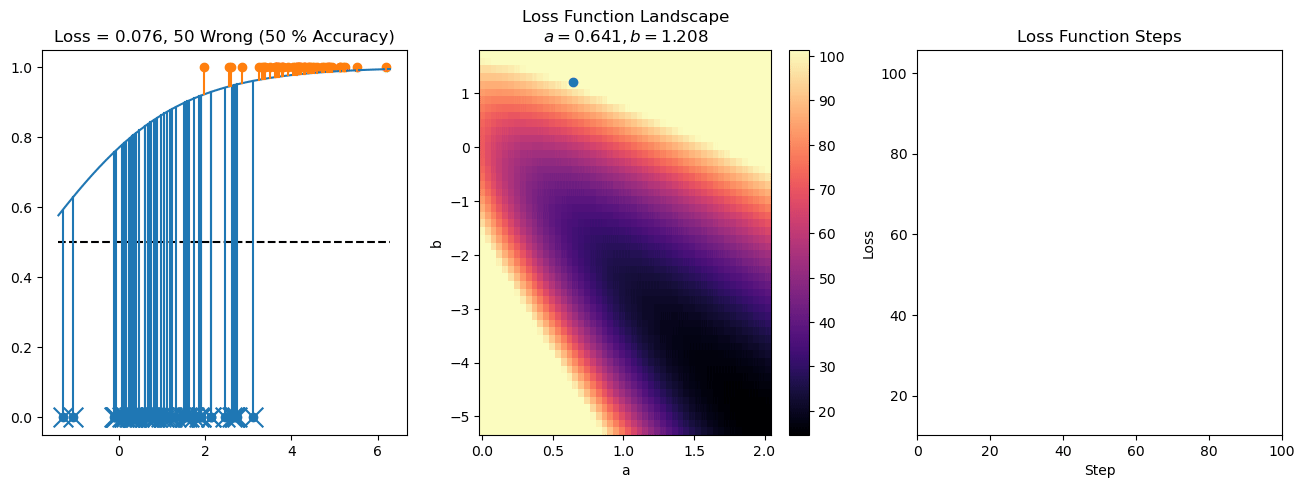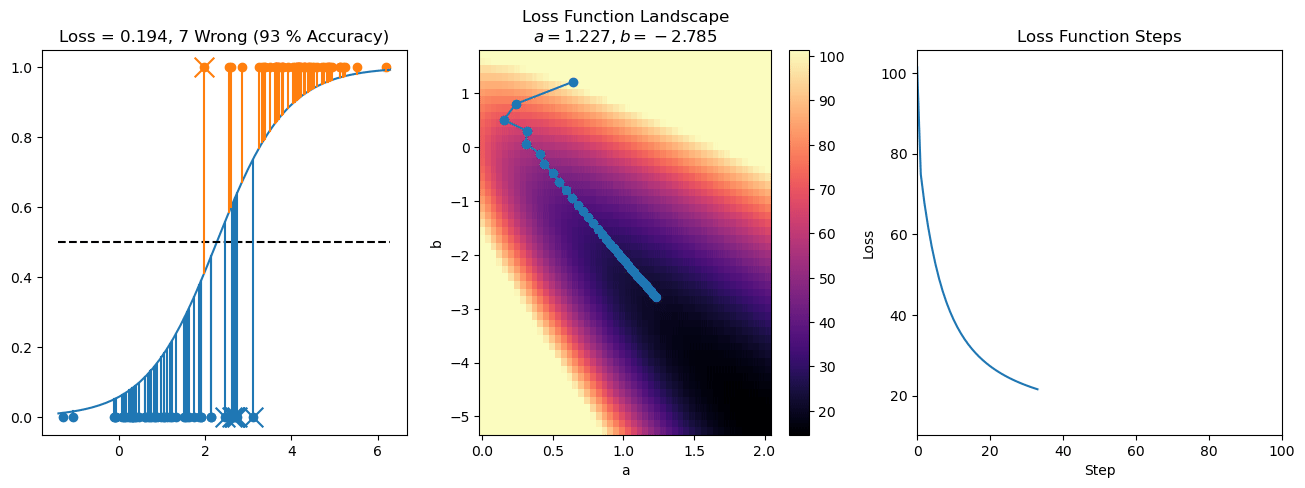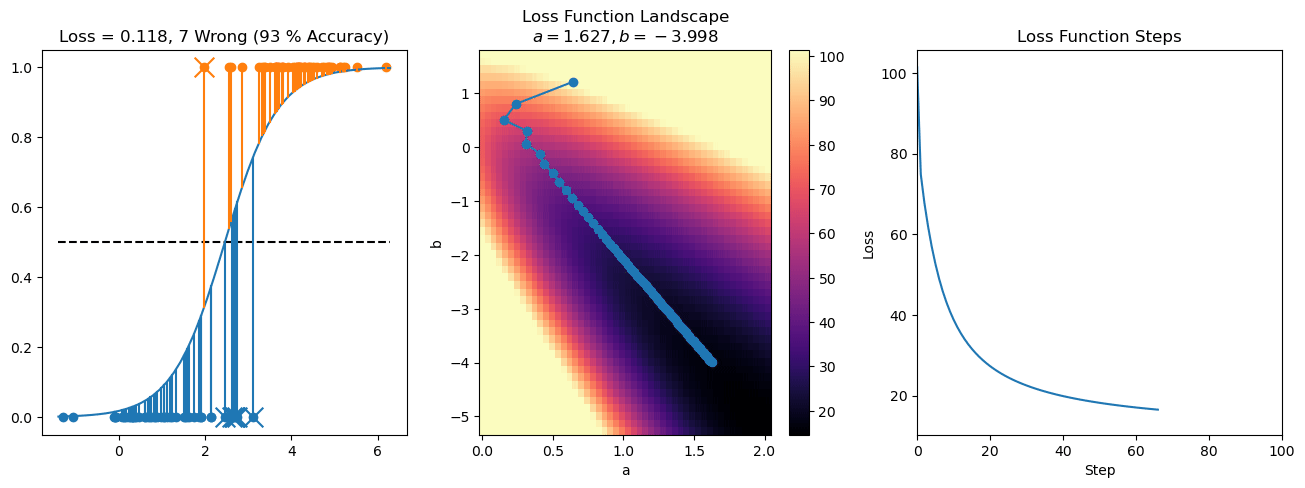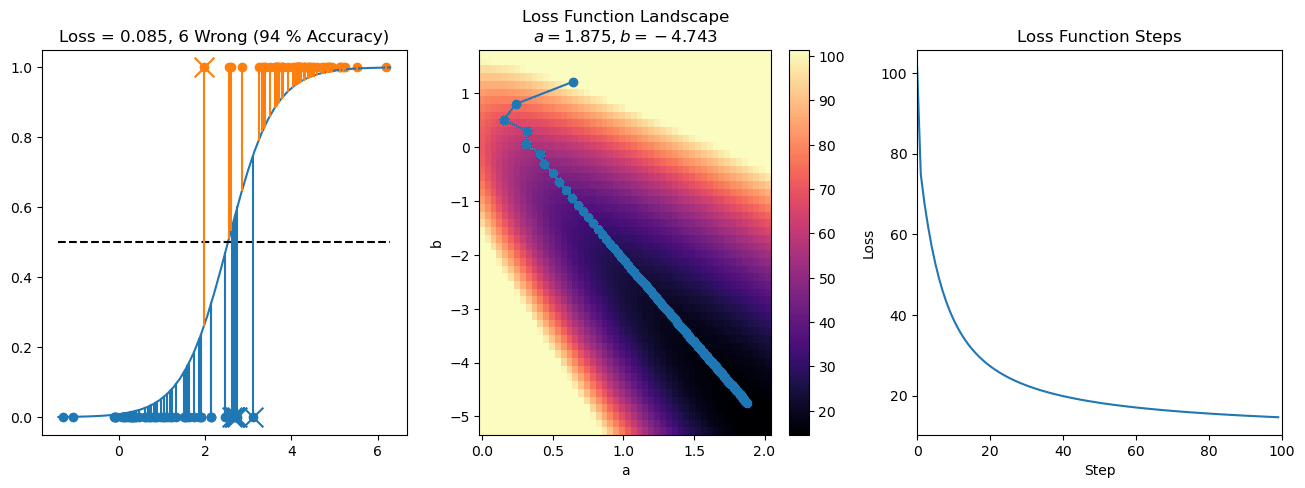
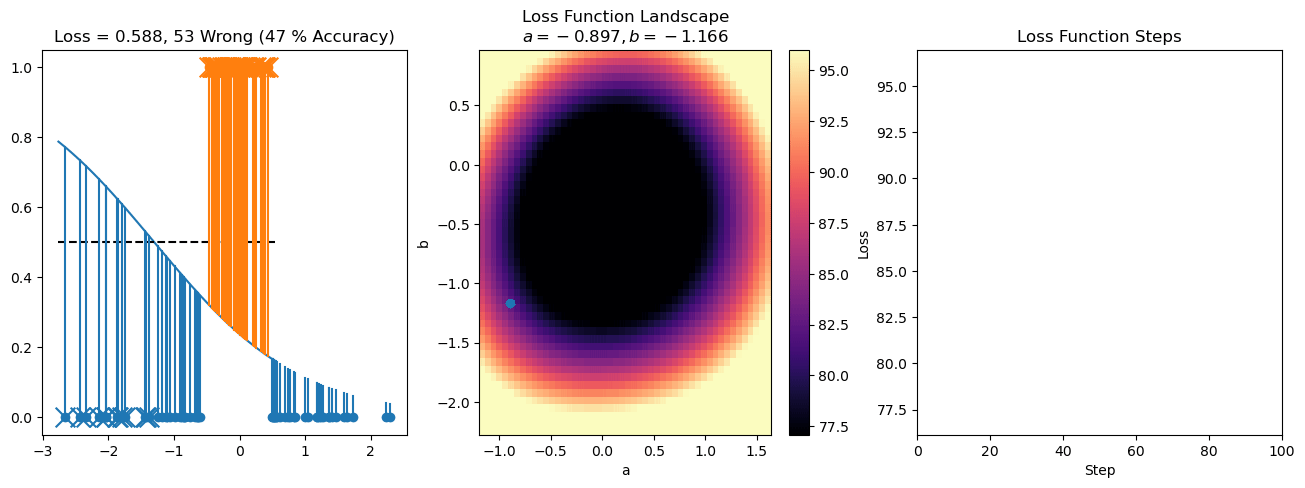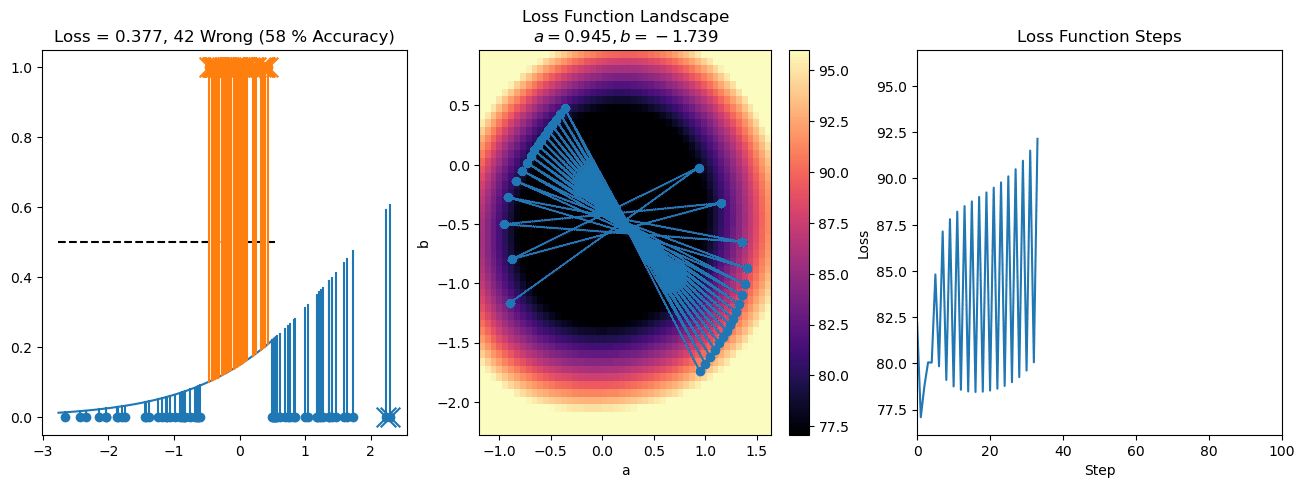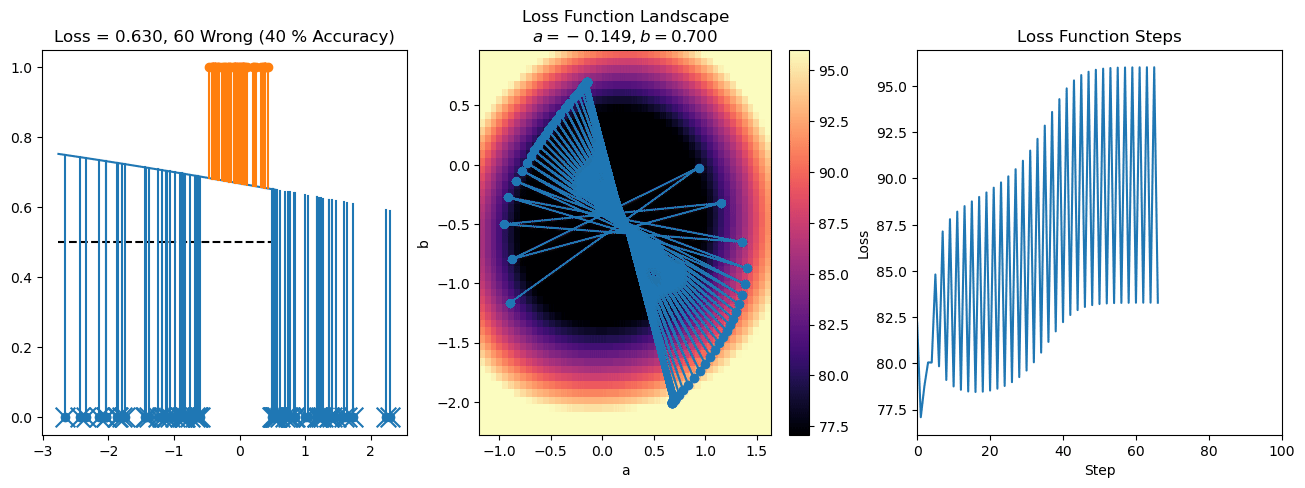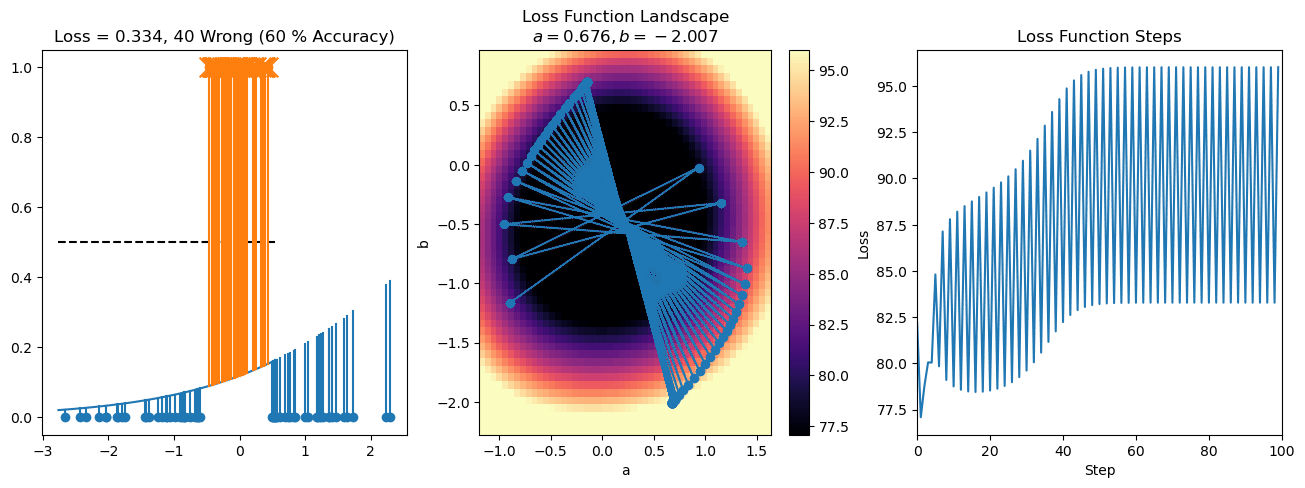
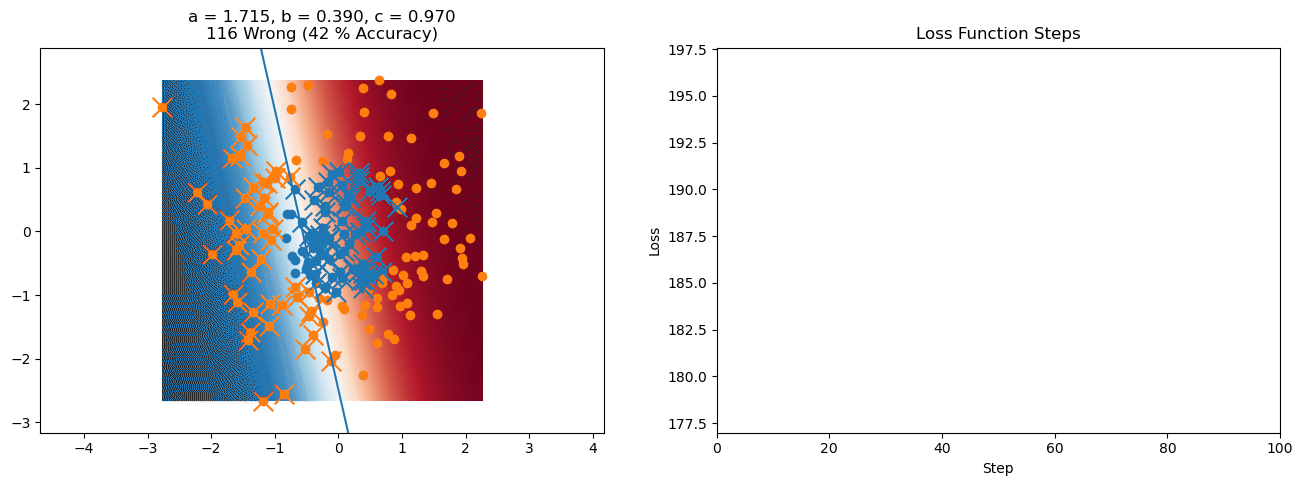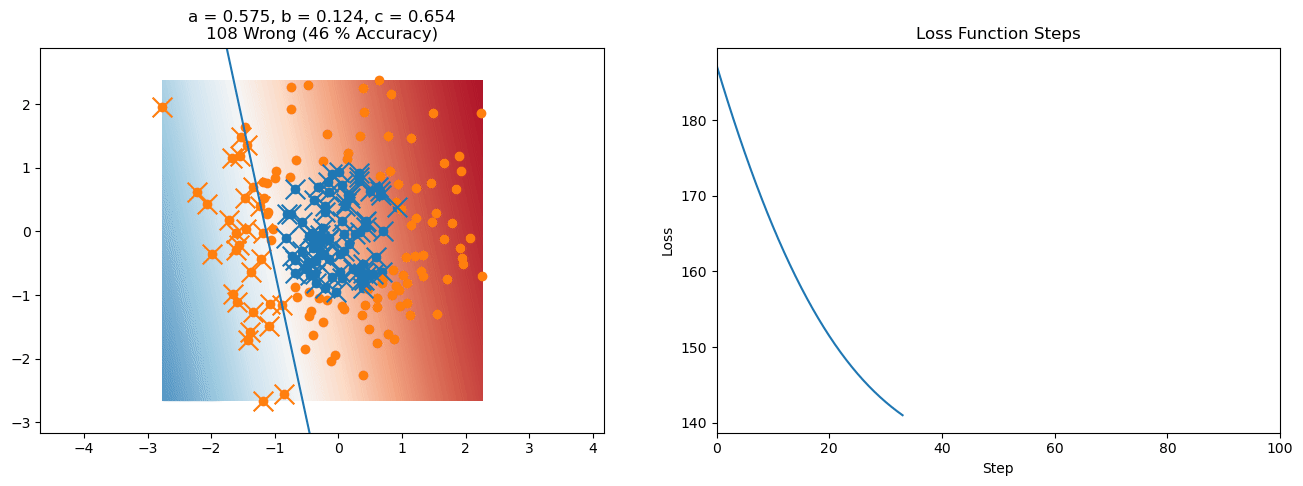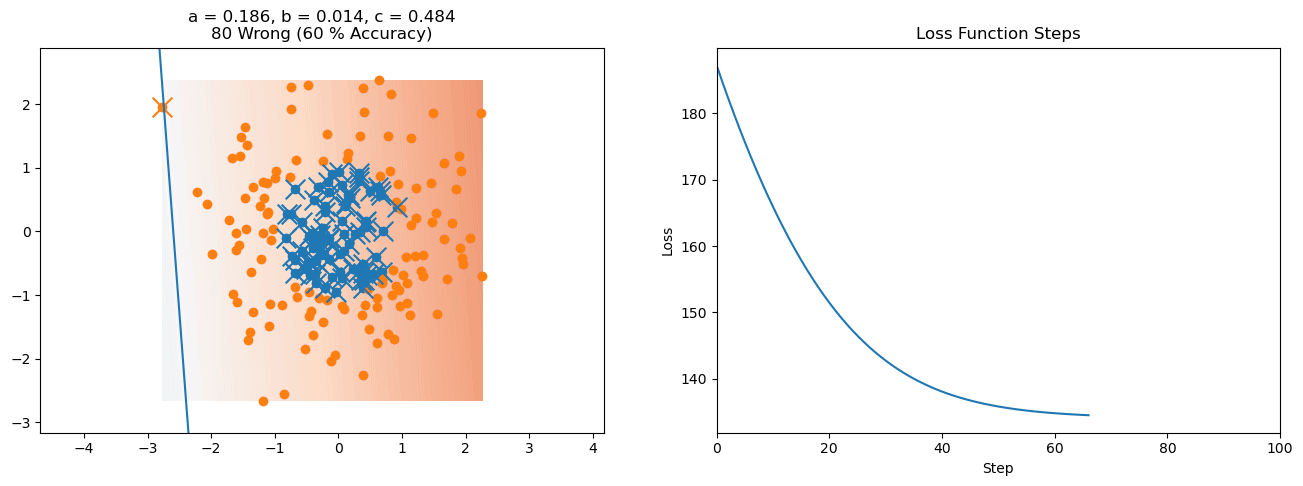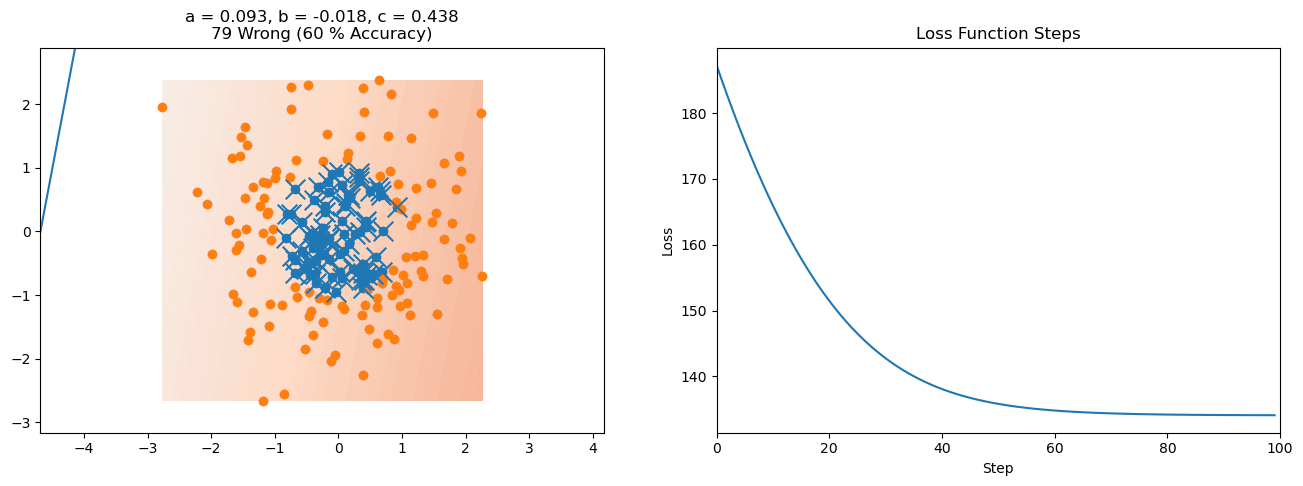
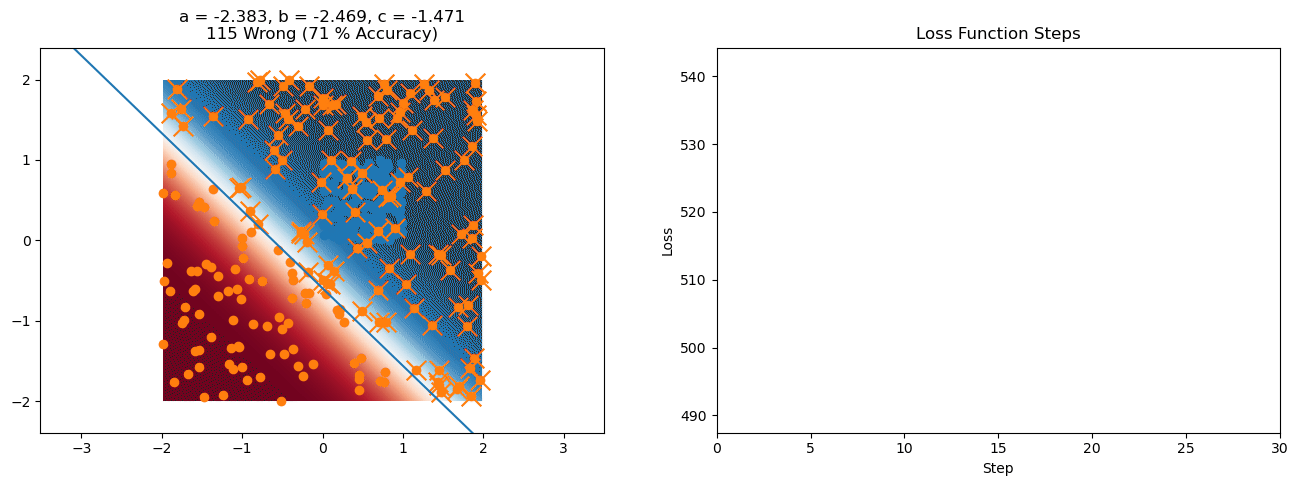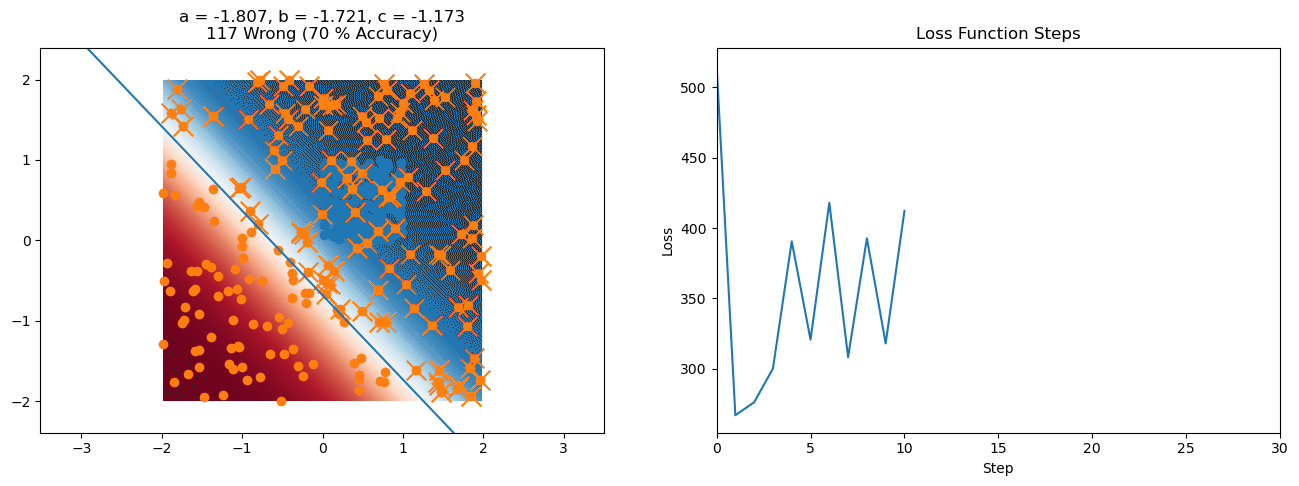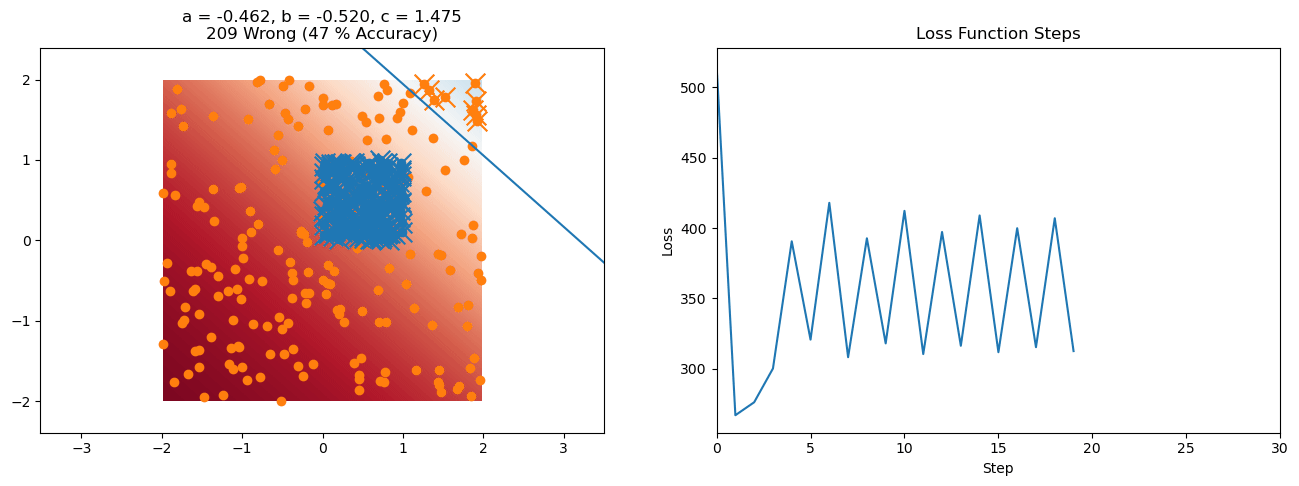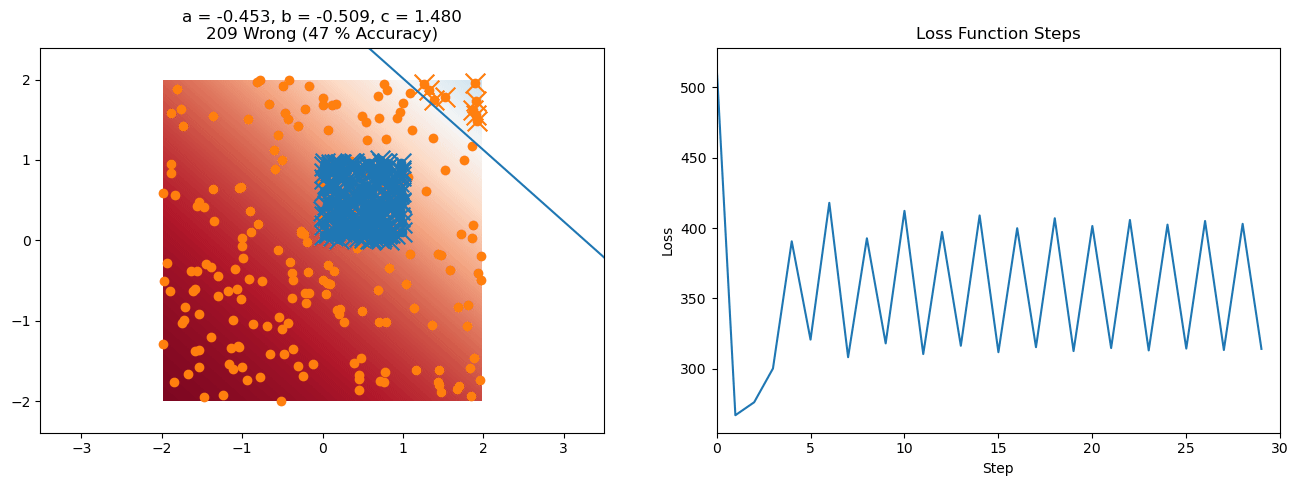
plt.title("a = {:.3f}, b = {:.3f}, c = {:.3f}\n{} Wrong ({} % Accuracy)".format(a, b, c, wrong, int(100*(N-wrong)/N)))
plt.axis("equal")
np.random.seed(0)
a_initial, b_initial, c_initial = np.random.randn(3)
lr = 0.01
n_iters = 20
# Example 1
#X0 = np.random.rand(100, 2) - np.array([[1, 0]]) # 100 0 examples between x = [-1, 0], y = [0, 1]
#X1 = np.random.rand(100, 2) + np.array([[0.5, 0]])
#X = np.concatenate((X0, X1), axis=0)
#y = np.zeros(X.shape[0])
#y[X0.shape[0]::] = 1
# Example 2
#X = np.random.randn(200, 2)
#r = np.sqrt(np.sum(X**2, axis=1))
#X0 = X[r < 1, :] # Examples that have radius < 1
#X1 = X[r >= 1, :] # Examples that have radius >= 1
#y = r >= 1
# Example 3
X0 = np.random.rand(200, 2)
X1 = 4*np.random.rand(200, 2) - 2
X = np.concatenate((X0, X1), axis=0)
y = np.zeros(X.shape[0])
y[X0.shape[0]::] = 1
losses = []
steps = []
a = a_initial
b = b_initial
c = c_initial
xmin = np.min(X, axis=0)
xmax = np.max(X, axis=0)
rg = xmax-xmin
xmin -= 0.1*rg
xmax += 0.1*rg
plt.figure(figsize=(16, 5))
for it in range(n_iters):
f = logistic(a*X[:, 0] + b*X[:, 1] + c)
a += lr*np.sum(X[:, 0]*(y-f))
b += lr*np.sum(X[:, 1]*(y-f))
c += lr*np.sum(y-f)
steps.append([a, b, c])
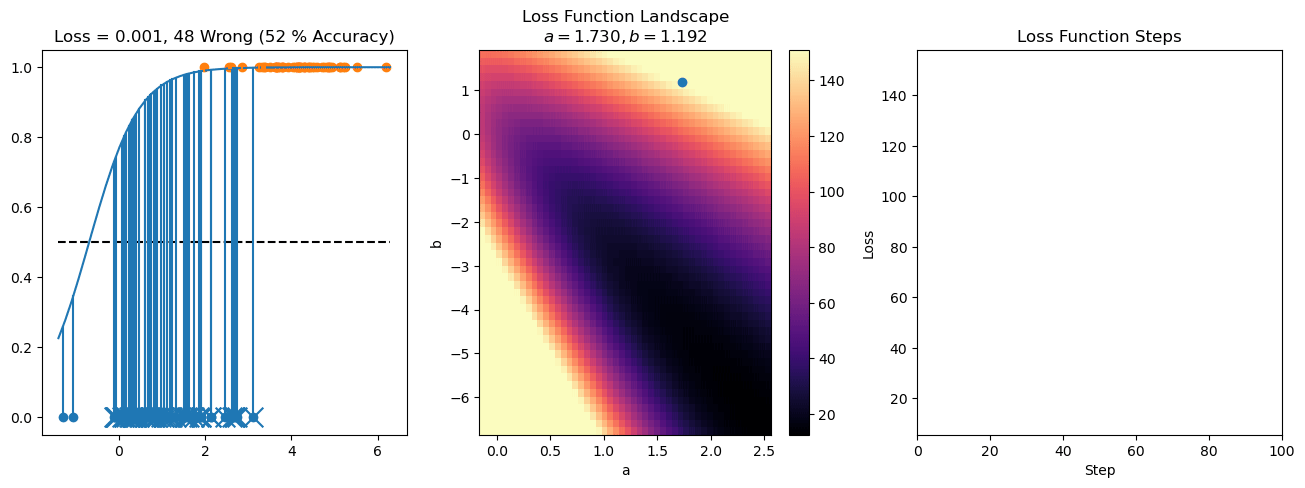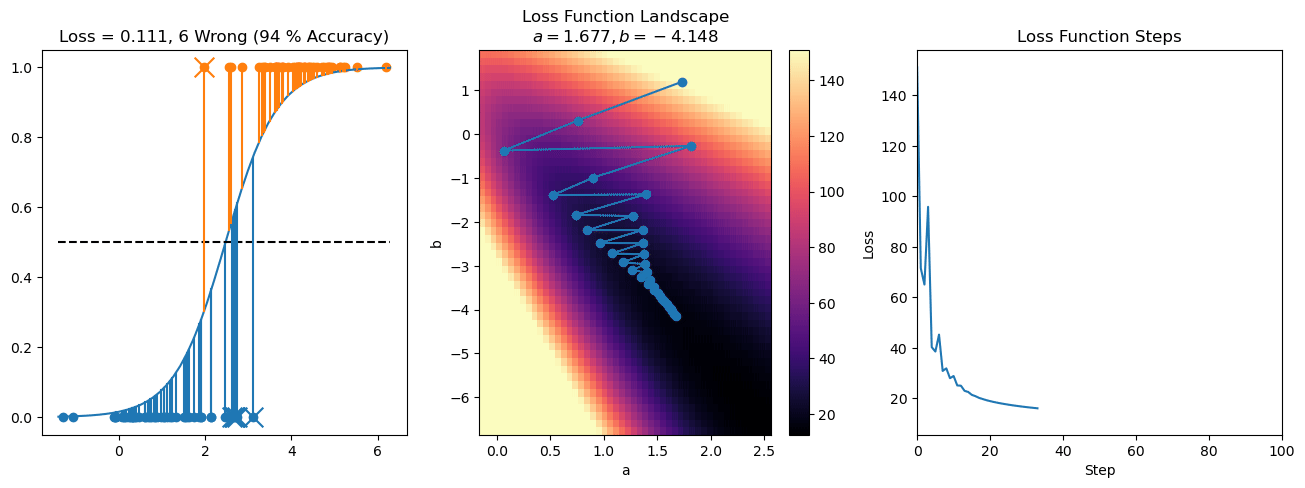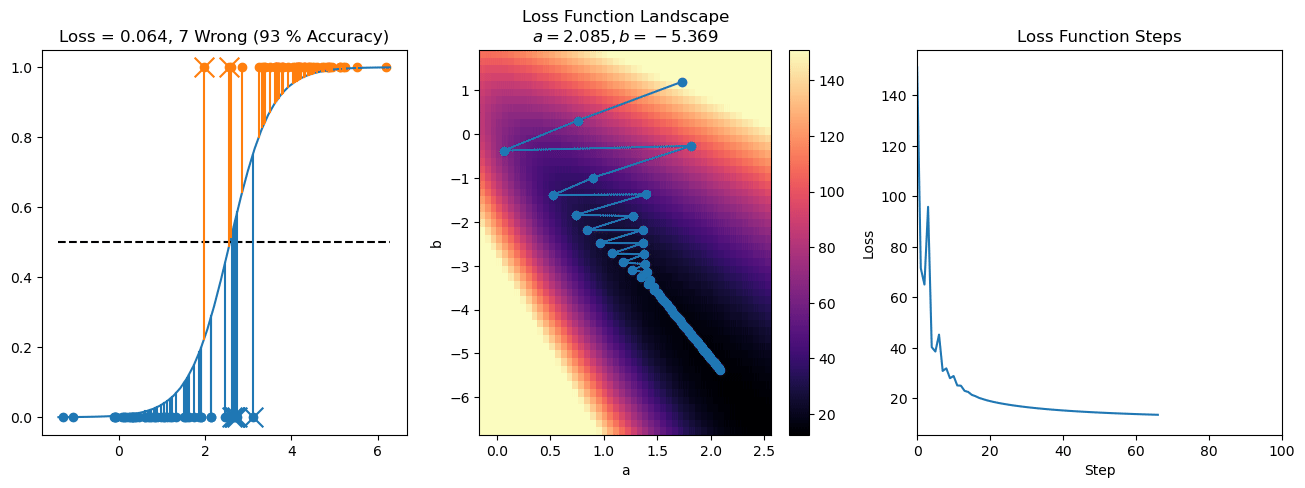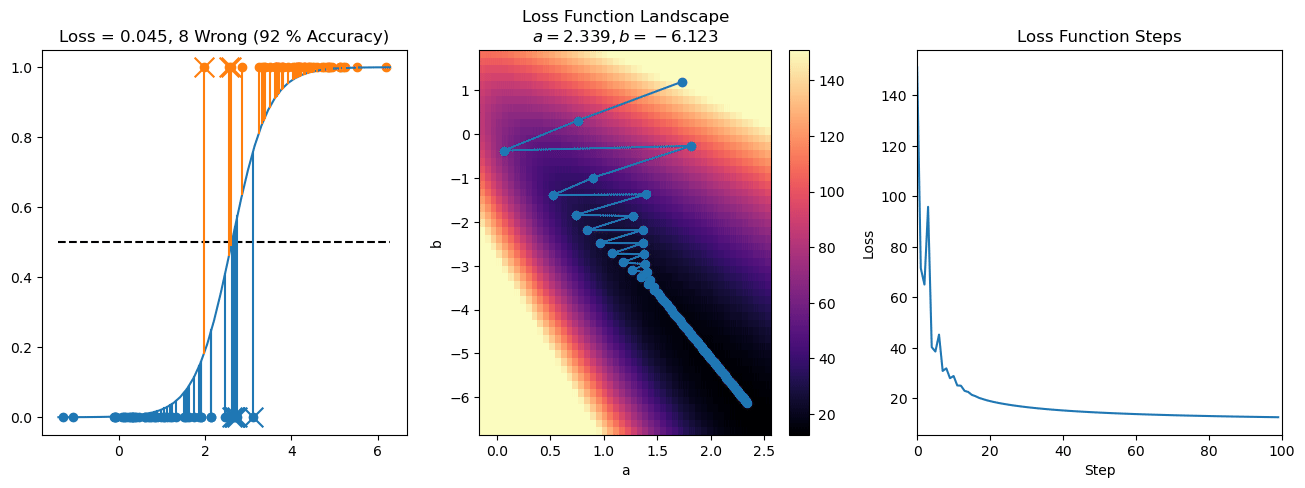
loss = np.sum(logistic_loss(a*X[:, 0] + b*X[:, 1] + c, y))
losses.append(loss)
plt.clf()
plt.subplot(121)
plot_logistic_regression_predictions(X0, X1, a, b, c)
plt.xlim(xmin[0], xmax[0])
plt.ylim(xmin[1], xmax[1])
plt.subplot(122)
plt.plot(losses)
plt.title("Loss Function Steps")
plt.xlabel("Step")
plt.ylabel("Loss")
plt.xlim([0, n_iters])
plt.savefig("Iter{}.png".format(it), facecolor='white', bbox_inches='tight')