Logistic Regression: Square vs Sawtooth

Chris Tralie

First, we create methods for generating square waves and sawtooth waves. We're careful to oversample and lowpass filter before downsampling to our desired sample rate to avoid aliasing. We have to be particularly careful with this, because we're going to be using a low sample rate of 8000hz to reduce the number of parameters that our models needs to tweak

import numpy as np
import matplotlib.pyplot as plt
import IPython.display as ipd
import torch
from torch import nn
from torch.utils.data import Dataset, DataLoader
from scipy import signal

def get_square(A, f, phi, sr, N, fac=10):
    # Compute antialiased square wave
    t = np.arange(N*fac)/(sr*fac)
    y = A*np.sign(np.cos(2*np.pi*f*t + phi))
    if fac > 1:
        # Antialias
        b, a = signal.butter(8, 1/fac)
        y = signal.filtfilt(b, a, y)
        y = y[0::fac]
    return y

def get_sawtooth(A, f, phi, sr, N, fac=10):
    T = sr*fac/f
    y = (np.arange(N*fac) + phi*T/(2*np.pi)) % T
    y = y/np.max(y)
    y = A*2*(y-0.5)
    if fac > 1:
        # Antialias
        b, a = signal.butter(8, 1/fac)
        y = signal.filtfilt(b, a, y)
        y = y[0::fac]
    return y

sr = 8000
y1 = get_sawtooth(2, 880, 0.5, sr, sr, fac=10)
y2 = get_square(2, 880, 0.5, sr, sr, fac=10)
plt.subplot(211)
plt.plot(y1[0:200])
plt.plot(y2[0:200])
plt.subplot(212)
plt.plot(np.abs(np.fft.fft(y1)))
plt.plot(np.abs(np.fft.fft(y2)), linestyle='--')
ipd.Audio(y1, rate=sr)

The Data Is Not Linearly Separable!

We note that a set of audio clips is linearly separable in its audio coordinate space if and only if it is linearly separable in the cosine/sine non-redundant DFT space. When we transform to the sine/cosine DFT space, we see what the problem is. We would have to separate the point at the origin from the annulus around it. So this dataset is not linearly separable

Below is the code I wrote to generate the above animation

sr = 8000 # Sample rate
N = 1000 # Number of audio samples per clip

n_frames = 150

fac = 1
plt.figure(figsize=(fac*15, fac*6))

T = 25 # Period
f = sr//25

idx = 2*f*N//sr
cidx1 = []
sidx1 = []
cidx2 = []
sidx2 = []

ylims = [-400, 400]

for i, phi in enumerate(np.linspace(0, np.pi, n_frames)):
    plt.clf()
    y1 = 0.6*get_square(1, f, phi, sr, N)
    f1 = np.fft.fft(y1)[0:N//2]
    y2 = get_sawtooth(1, f, phi, sr, N)
    f2 = np.fft.fft(y2)[0:N//2]
    
    cidx1.append(np.real(f1)[idx])
    sidx1.append(np.imag(f1)[idx])
    cidx2.append(np.real(f2)[idx])
    sidx2.append(np.imag(f2)[idx])
    
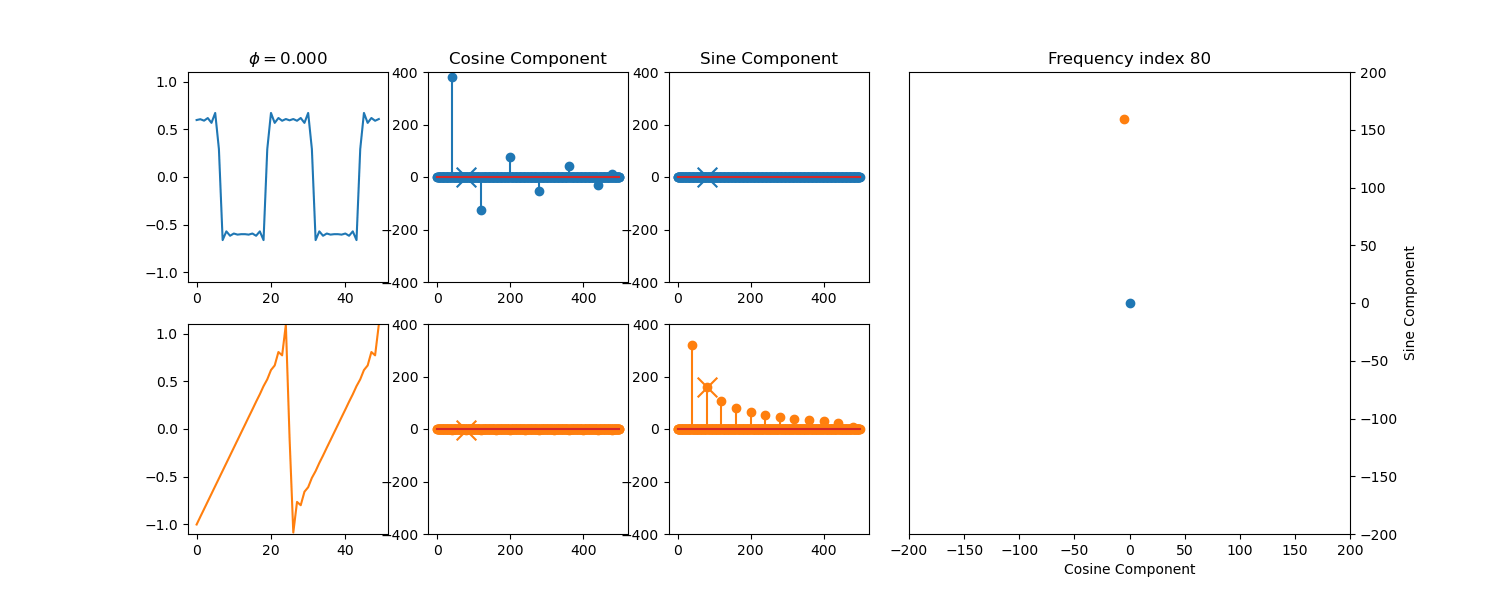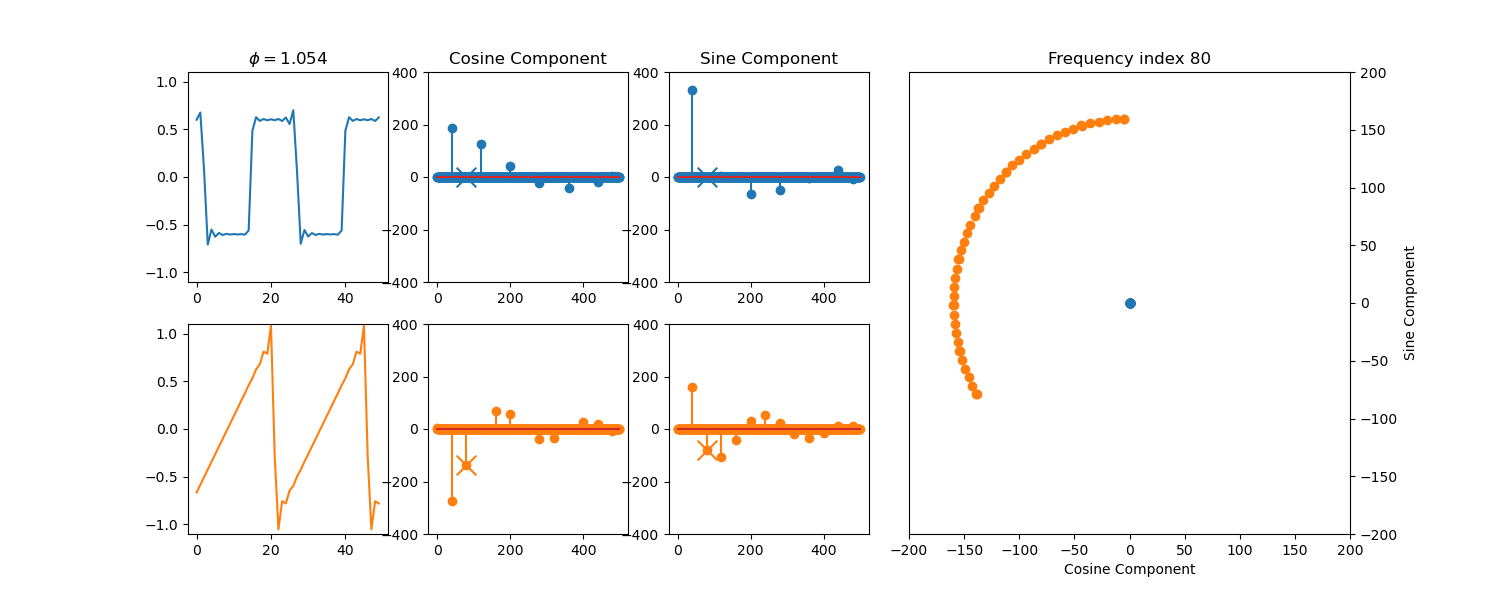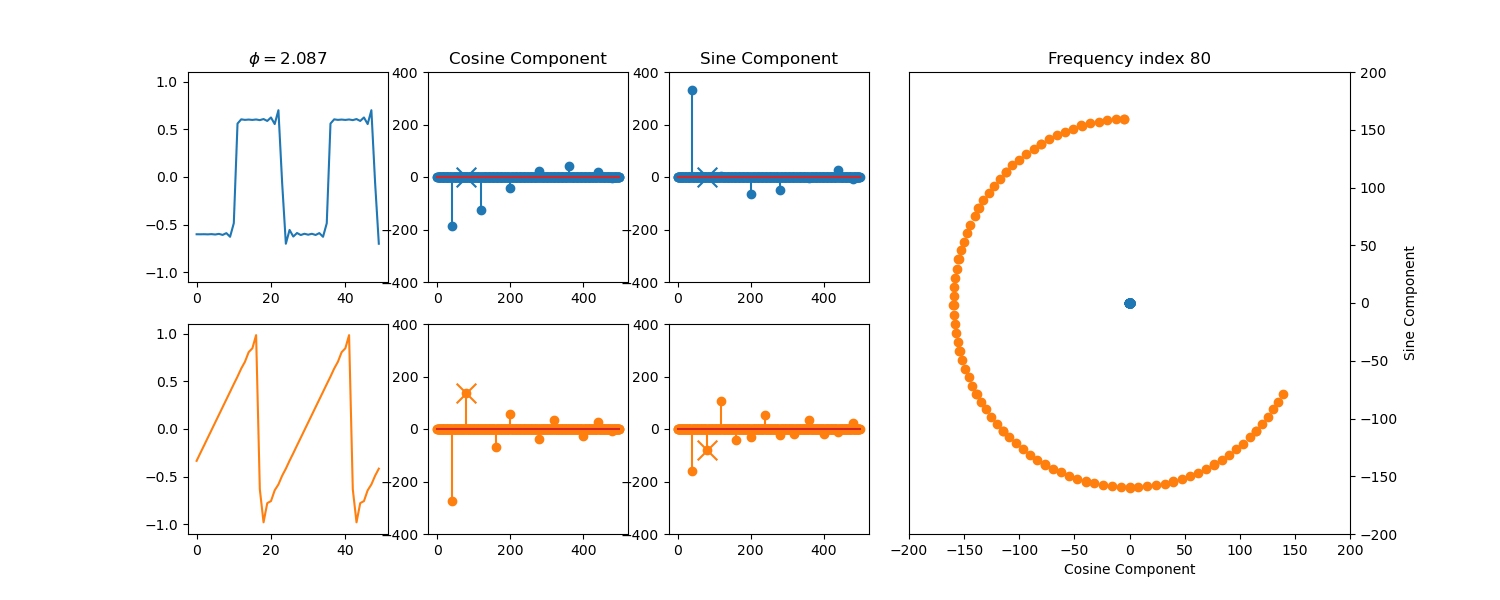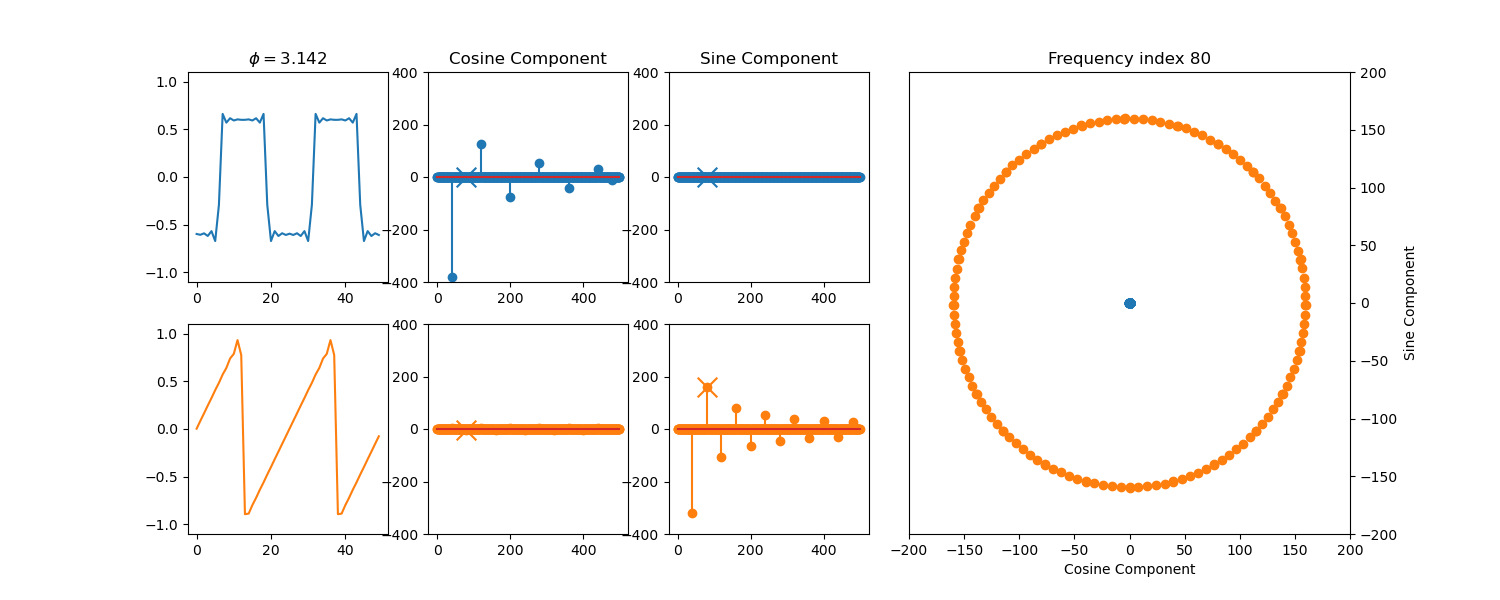
    plt.subplot(251)
    plt.plot(y1[0:50])
    plt.title("$\\phi = {:.3f}$".format(phi))
    plt.ylim([-1.1, 1.1])
    plt.subplot(252)
    plt.stem(np.real(f1))
    plt.scatter(idx, cidx1[-1], s=200, c='C0', marker='x')
    plt.ylim(ylims)
    plt.title("Cosine Component")
    plt.subplot(253)
    plt.stem(np.imag(f1))
    plt.scatter(idx, sidx1[-1], s=200, c='C0', marker='x')
    plt.ylim(ylims)
    plt.title("Sine Component")
    
    plt.subplot(256)
    plt.plot(y2[0:50], c='C1')
    plt.ylim([-1.1, 1.1])
    plt.subplot(257)
    markerline, stemlines, baseline = plt.stem(np.real(f2))
    plt.setp(markerline, 'color', 'C1')
    plt.setp(stemlines, 'color', 'C1')
    plt.scatter(idx, cidx2[-1], s=200, c='C1', marker='x')
    plt.ylim(ylims)
    plt.subplot(258)
    markerline, stemlines, baseline = plt.stem(np.imag(f2))
    plt.setp(markerline, 'color', 'C1')
    plt.setp(stemlines, 'color', 'C1')
    plt.scatter(idx, sidx2[-1], s=200, c='C1', marker='x')
    plt.ylim(ylims)
    
    plt.subplot2grid((2, 5), (0, 3), rowspan=2, colspan=2)
    plt.scatter(cidx1, sidx1)
    plt.scatter(cidx2, sidx2)
    plt.xlim(-200, 200)
    plt.ylim(-200, 200)
    plt.title("Frequency index {}".format(idx))
    plt.xlabel("Cosine Component")
    plt.ylabel("Sine Component")
    plt.gca().yaxis.set_label_position("right")
    plt.gca().yaxis.tick_right()
    
    plt.savefig("shift{}.png".format(i))

<Figure size 1500x600 with 0 Axes>

To make this linearly separable, we'll replace the input array with the magnitude of its fourier transform. This throws away the phase as a nuisance parameter

Data Loader

class SquareSawtooth(Dataset):
    def __init__(self, n_examples, pmin, pmax, sr, N, snr=10, do_fft=False):
        """
        Parameters
        ----------
        n_examples: int
            Number of examples per epoch
        pmin: int
            Minimum note number
        pmax: int
            Maximum note number
        sr: int
            Sample rate
        N: int
            Number of samples per example
        snr: float
            Signal to noise ratio
        """
        # Create randomized fixed notes
        self.pmin = pmin
        self.pmax = pmax
        self.snr = snr
        self.sr = sr
        self.N = N
        self.n_examples = n_examples
        self.do_fft = do_fft
    
    def __len__(self):
        return self.n_examples
    
    def __getitem__(self, idx):
        ## If the sample index is even, generate a random square wave with label 0
        ## If the sample index is off, generate a random sawtooth wave with label 1
        y = idx % 2
        A = np.random.randn()
        phi = 2*np.pi*np.random.rand()
        f = 440*2**(np.random.randint(self.pmin, self.pmax+1)/12)
        if y == 0:
            x = get_square(A, f, phi,self.sr, self.N, fac=10)
            x += A*np.random.randn(x.size)/self.snr
        else:
            x = get_sawtooth(A, f, phi,self.sr, self.N, fac=10)
            x += A*np.random.randn(x.size)/self.snr
        if self.do_fft:
            # Throw away the phase
            x = np.abs(np.fft.fft(x))
        x = torch.from_numpy(np.array(x, dtype=np.float32))
        y = torch.from_numpy(np.array(y, dtype=np.float32))
        return x, y

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print("Device", device)

sr = 8000 # Sample rate
N = 1000 # Number of audio samples per clip

p1 = 0
p2 = 0
data = SquareSawtooth(1000, p1, p2, sr, N, snr=10, do_fft=True)

Device cuda

## TODO: Setup a perceptron of the right dimension
perceptron = nn.Linear(N, 1)
perceptron = perceptron.to(device)
optimizer = torch.optim.Adam(perceptron.parameters(), lr=1e-2)
loss_fn = torch.nn.BCEWithLogitsLoss()


n_epochs = 50
losses = []
accuracy = []
plt.figure(figsize=(12, 6))
for epoch in range(n_epochs):
    loader = DataLoader(data, batch_size=32, shuffle=True)
    total_loss = 0
    total_correct = 0
    for i, (X, Y) in enumerate(loader):
        X = X.to(device)
        Y = Y.to(device)
        optimizer.zero_grad()
        Y_est = perceptron(X) # Run model on inputs
        loss = loss_fn(Y_est[:, 0], Y) # Compute loss function
        loss.backward() # Compute gradient of loss function wrt model parameters
        optimizer.step() # Update the parameters according to the gradient
        
        loss = loss.item()
        total_loss += loss
        Y_est = 0.5*(torch.sign(Y_est[:, 0]) + 1) # 1 if estimate is 1, 0 otherwise
        total_correct += torch.sum(Y_est == Y)
    
    a = total_correct.cpu().detach()/len(data)
    losses.append(loss)
    accuracy.append(a)

    #print("Epoch {}, loss = {:.3f}, accuracy={:.3f}".format(epoch, loss, a))

<Figure size 1200x600 with 0 Axes>

## Plot the results of training
plt.figure(figsize=(10, 5))
plt.subplot(211)
plt.plot(losses)
plt.title("Losses")
plt.xlabel("Epoch Number")
plt.ylabel("Loss")

plt.subplot(212)
plt.plot(accuracy)
plt.title("Accuracy")
plt.xlabel("Epoch Number")
plt.ylabel("Loss")
plt.tight_layout()

Recall that the input to the logistic function is

$a_0x[0] + a_1x[1] + a_2x[2] + ... + a_{d-1}x[d-1] + b$

We want this to be negative for a square wave and positive for a sawtooth wave. The training learns that if it makes the coefficients in front of the frequencies that they both have in common to be negative, and the frequencies in front of the coefficients that only the sawtooth wave has, then it works! And we didn't even tell it that these FFTs had equally spaced harmonics, let alone that the sawtooth wave had more than the square wave!

# 0 is square
# 1 is sawtooth
x0 = data[0][0]
x1 = data[1][0]
p, b = list(perceptron.parameters())
p = p.cpu().detach().flatten()
b = b.cpu().detach().flatten()
print("bias", b)
plt.figure(figsize=(12, 6))
plt.subplot(311)
plt.plot(x0, c='C0')
plt.title("Square Wave Example")
plt.subplot(312)
plt.plot(x1, c='C1')
plt.title("Sawtooth Wave Example")
plt.subplot(313)
plt.plot(p, c='C2')
plt.plot(np.zeros(len(p)), c='k', linewidth=2)
plt.title("Logistic Coefficients")
plt.tight_layout()

bias tensor([0.1371])